Die allgemeine Transportgleichung in koordinatenfreier Form mit den Termvariablen φ,Γφ, qφ :
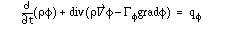
Es wird die Struktur von Worten einer Sprache als Abstraktion identifiziert. Dann werden theoretische und praktische Anwendungen vorgestellt.
Die syntaktischen Komponenten einer Formel in der Mathematik oder Physik sind Konstanten, (arithmetische,Differential-,...) Operatoren, Funktionssymbole, und Variablen (sowohl für Konstanten als auch für Funktionssymbole).
Die zulässigen Formeln sind Wörter einer Sprache, z.B. der mathematischen Formelsprache. Solche Sprachen lassen sich meist durch eine kontextfreie Chomsky-Grammatik beschreiben:
Eine kontextfreie Chomsky-Grammatik ist ein Tupel G = (T,N,P,S) mit
Die von der Grammatik G erzeugte Sprache ist L( G) := {w ∈ T* | S →* w }
Umfangreiche Rechnungen (Umformungen) lassen sich leichter bewältigen, wenn man länglichere Teilausdrücke durch neueinzuführende Symbole ersetzt. Am Ende der Rechnung werden diese Symbole wiederum durch den Teilausdruck ersetzt. Diese Symbole werden Termvariablen genannt. Dies wollen wir verallgemeinern:
Eine Variable ist ein Symbol, das durch Individuen eines Grundbereichs ersetzt werden darf. Dieser Grundbereich heißt Typ der Variable.
Die obigen Symbole sind Variablen mit dem Grundbereich Terme2
, also Termvariablen. Es soll aber nicht zulässig sein, Termvariablen etwa durch beliebige Formeln zu ersetzen.
(Terme bestehen als Konstanten, Variablen und Rechenoperationen. In atomare Formeln werden kommen Terme und Relationen vor. Atomare Formeln werden mit logischen Operationen und Quantoren zu Formeln verknüpft. Formeln sind also Aussagen bzw. Aussageformen, wenn noch freie,d.h ungebundene Variablen vorkommen).
Stellt man für Formeln eine Grammatik auf, so wird man ein nichtterminales Symbol haben, das die Terme repräsentiert. Dieses Termsymbol kann man auch als Startsymbol einer Teilgrammatik auffassen.
Da liegt folgende Definition nahe:
Ω sei die Menge aller Wortvariablen beliebigen Typs.
Es gelte Ω ∩ ( T ∪ N) = ∅
Die Funktion Typ: Ω → N liefere den Typ einer Wortvariablen 3 : Typ(ω)=N
ΩN := { ω ∈ Ω | Typ(ω) = N }
sei die Menge aller Wortvariablen vom Typ N
Die Typfunktion werde so auf Wörter mit Wortvariablen erweitert, daß im Wort jede Wortvariable durch das Nichtterminalsymbol ersetzt wird, dessen Typ sie hat:
Typ:( T ∪ Ω)* → V*
Typ(w)=v ⇒ i=1,...,|w|: ((wi ∈ T ⇒ wi = vi) ∧ (wi ∈ Ω ⇒ vi =Typ(wi))) ∧ |w|=|v|
LΩ = L(GΩ) sei die Erweiterung der Sprache mit den Wortvariablen.
Die Ersetzung von Wortvariablen in einem Wort aus LΩ durch Wörter entsprechenden Typs nennt man Substitution.
Eine Substitution
σ wird auf einer Menge A ⊆ Ω von Wortvariablen definiert.Terminalsymbole bleiben stehen: ∀ t ∈ T : σ(t)=t
Für Wörter w ∈ (T∪Ω)* : σ(w)
= Xi=1,...,|w|σ(wi)
(X sei die wiederholte Konkatination ähnlich dem Summenzeichen Σ
für die Summation : Xi=1..n wi := w1w2...wn
Bemerkung:
Man kann Substitutionen als Funktionen von Variablen in Wörter auffassen und die Erweiterung als Funktion von Wörtern in Wörtern:
σ : LΩ → LΩ
Die Konstruktion aus Wortvariable vom Typ eines Nichtterminalsymbols und Substitutionen stellt dies sicher.
Wenn durch Substitution von Teilwörtern durch Wortvariablen mehrere verschiedene Wörter gleich gemacht werden können, so kann man sagen, daß sie die gleiche Struktur haben. Dann kann eine Äquivalenzrelation "Strukturgleichheit" eingeführten. Damit kann man auch begründet von Abstraktion sprechen. Das durch die Substitution mit den Wortvariablen erhaltene Wort kann man dann abstraktes Wort nennen.
Wenn durch die Rücksubstitution die Variablen wieder durch Teilwörter ersetzt werden, kann man das auch als Spezifikation (Artbildung) auffassen. Damit hat man nach der ursprünglichen Wortbedeutung den Begriff "Art", und dazu gehört ja auch nach der antiken Definitionslehre (vgl. [Wede92] S.31) eine Gattung.
Damit haben wir die Art-Gattungs- oder Subordinationsbeziehung zwischen Wörtern
.
Diese Beziehung von Art zur Gattung wird oft Generaliserung und die von Gattung zur Art wird auch Spezialisierung genannt.
Gegeben seien zwei Objekte 5 x und y.
Gesucht ist ein drittes Objekt z von denen sowohl x als auch y Instanzen sind
Die Ersetzung von Teilwörtern durch Wortvariablen wird laut Knight "Antisubstitution" genannt.
Da es nicht sinnvoll ist, willkürlich Teilwörter aus Wörtern einer Sprache zu ersetzen, gelten die selben Bedingungen wie für Substitutionen:
Sei G eine Grammatik, w ∈ L(GΩ) und γ eine Antisubstitution.
Es sollte gelten:Seien v,w ∈ LΩ. v und w sind generalisierbar (generalizable), wenn eine Antisubstitution γ existiert, so daß γ(v) = γ(w).
γ heißt dann Generalisierer von v und w.
Die Generalisierung von Wörtern ist an sich nichtssagend, weil zwei Wörter v und w immer durch eine Antisubstitution γ = {v → ζ , w → ζ }
auf triviale Weise generalisiert werden können (Typ(ζ) = S).
Es interessiert aber, welcher Generalisierer am meisten Struktur übrig läßt:
Ein Generalisierter γ von v,w heißt der speziellste Generalisierer (most spezific generalisizer), falls es für jeden anderen Generalisierter η eine Antisubstitution ν gibt, so daß
Intuitiv enthält die speziellste Generalisierung von zwei Wörtern die Information, die in beiden Wörtern enthalten ist und führt neue Wortvariablen dort ein, wo die Wörter voneinander abweichen.
Bemerkung: In [Reyn70] wurde die Existenz für einen eindeutigen speziellsten Generalisierer für first-order Terme bewiesen und ein Algorithmus zur Ermittlung angegeben. Plotkins hat unabhängig in [Plotk70] einen ähnlichen Algorithmus entdeckt.
Mit diesem können wir nun formal die Abstraktion "Struktur" einführen:
Nach [Lor87] S. 163 ist die Abstraktion die Beschränkung auf invariante Aussagen bezüglich einer Äquivalenzrelation ˜.
Sei also σ der speziellster Generalisierer der Wörter w1 und w2.
Dann haben wir die Äquivalenzrelation
Für alle bzgl. ˜σ invarianten Ausgeformen A mit
Diesen speziellsten Generalisierer σ kann man nun "Strukturabstraktor" nennen.
Diese mit der oben beschriebenen Methode erhaltenen Beziehungen kann man auch ausnutzen, um die Wörter übersichtlich aufzuschreiben:
Man schreibt erst das abstrakte, generalisierte Wort auf, und dann die Wertetabelle der Substitutionsfunktionen, die das abstrakte Wort zu den spezielleren Wörtern substituiert.
Beispiel:
Die Tabelle 1 im Abschnitt 3.4 in [Weber93] dient hier als klassisches Beispiel aus der Strömungsmachanik:
Die allgemeine Transportgleichung in koordinatenfreier Form mit den Termvariablen φ,Γφ, qφ :
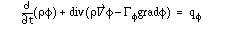
Die verschiedenen Transportgleichungen ergeben sich aus folgender Tabelle:
Weitere praktische Beispiele findet man in [Weber93] .
Jede abstrakte Formel wird in eine Klasse geschrieben. Manchmal ist es sinnvoll, für eine Formel eine eigene Klasse zu bilden, auf alle Fälle gehört die Formel zu irgendeiner Klasse.
Die zu substituierenden Variablen mit Name V
der abstrakten Formel in der Oberklasse ergeben eine virtuelle Operation namens berechneV , die in einer Unterklasse realisiert wird.
In der abstrakten Formel in der Oberklasse werden die Vorkommen der Variablen V dann durch Aufrufe der Operation berechneV ersetzt.
Der Vorteil liegt in der Wiederverwendung von Programmteilen, die nur einmal geschrieben und ausgetestet werden brauchen.
Leider wird diese Implementierungstechnik einen nicht vertretbaren hohen Laufzeitaufwand verursachen, da die konkreten Funktionen zur Laufzeit bestimmt und dann aufgerufen werden müssen (virtuelle Funktion in C++). In C++ erfolgt dies zwar sehr effizient (Zugriff auf Feld von Funktionszeiger über Index, dann Aufruf), dies ist jedoch viel mehr als die direkte Ausführung des Codes.
Dies kann jedoch einfach vom Compiler optimiert werden, wenn er die Hierarchieen einebnet, d.h in einer konkreten Klasse die Variablen und Funktionen der Oberklassen implementiert, so daß die Vererbung entfällt.
Wenn man einen Algorithmus oder einen Typ auf verschiedene Weise implementieren will, kann man oft eine gemeinsame Aufrufschnittstelle herstellen. Hier liegt also wieder eine Abstraktion vor.
Dies kann man nun auf 3 verschiedene Arten realisieren:
Hier werden Designalternativen als Unterklasse im objektorientierten Sinne formuliert und entsprechend instanziert.
Hier beschreiben Variablen welcher Algorithmus gewählt wird, die dann an Stellen, an den sich die Alternativen unterscheiden, auf die verschiedenen Alternativen verzweigt wird (vgl. Giantsimulator Modul wuerfel.c von Ronald Lange, verschiedener Kraftalgorithmus bei Molekulardynamikprogramm)
In diesem Fall werden separate Module geschrieben, die dann entsprechend zusammengelinkt werden.
Voraussetzung ist, daß im selben Programm nur eine Alternative benötigt wird.
Hierzu empfiehlt es sich, die Verzeichnisstruktur des Quellcodebaumes als Vererbungshierarchie anzulegen. Es gibt Quellcodedateien, die in jeder Alternative neu Übersetzt werden müssen. Dies Kann man in UNIX-Dateisystemen dadurch erreichen, daß man einen sog. Softlink zum Original setzt, der nach dem Übersetzen wieder entfernt wird.
Mit C-Präprozessordirektiven (
#ifdef BEDINGUNG //... #else ... #endif) kann man leicht voneinander abweichende Programmteile verschiedener Versionen in demselben Modul realisieren, was dann je nach benötigter Version verschieden übersetzt wird.
Die "Wörter" aus dem Theoretische Fundierung können natürlich auch beliebige Funktionen bzw. Prozeduren oder sogar ganze Programme sein.
Für den Bereich der parallelen technisch-wissenschaftlichen Programme liegt die Idee nahe, die Parallelitätsstruktur aus den Programmtexten zu abstrahieren.
Bei der genaueren Betrachtung der Mathematik stellt man fest, daß z.B Begriffe wie "Gleichungssystem","lineares Gleichungssystem" mit Hilfe der Strukturgleichheit gebildet werden.
Ein weiteres Beispiel sind die oben erwähnten Transportgleichungen. Der aufmerksame Leser wird viele weitere Beispiele in der mathematischen Literatur finden.
In Grammatiken, Wortvariablen und Substitutionen wurde als Motivationsbeispiel erwähnt, wie man sich durch die Einführung von Wortvariablen bei formalen Rechnungen und Beweisen die Arbeit übersichtlicher gestalten und somit vereinfachen kann. Mit der obengenannten Anwendung kann man sich Arbeit ersparen.
In [Weber93] wurde (wie auch schon in der strömungsmechanischen Literatur wie [Plotk70]) zuerst solange wie möglich mit der allgemeinen Transportgleichung (bei der Diskretisierung) gerechnet, dann erst mit den speziellen weitergerechnet.
Es wurde auch so lange wie möglich koordinatenfrei (mit Vektoren, Divergenz,...) gerechnet, und erst möglichst spät der zweidimensionale kartesische Fall betrachtet.
Sei A seine Aussagenform in der Aussagenlogik und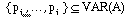 
und B1,...,Bk
Aussageformen.
B sei diejenige Aussageform, die aus A entsteht, wenn man simultan alle Vorkommen von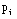 
durch Bj
ersetzt.
Dann gilt: Wenn A eine Tautologie ist, so ist auch B Tautologie
(Strehl ,Kap. I Abschnitt 15 S. 15)
Bemerkung :
Das simultane Ersetzen ist wichtig:
z.B ist A(p1 →(p2) →p1)) eine Tautologie.
Das simultane Ersetzen von p 1
durch p 2 liefert die Tautologie (p 2 →(p 2 →p 2))
Ersetzt man jedoch nur das erste Vorkommen von p
1 , so erhält man (p 2 →(p 2 →p 1)), was keine Tautologie mehr ist (man bewerte p 1 mit "falsch" und p 2 mit "wahr").
([Strehl] , Kap. I, Abschnitt 17)
Es ist also Vorsicht angesagt!
Seien A,A',B,B' Ausgabeformen, wobei A' aus A entsteht, in dem man einige (also beliebig viele) Vorkommen von B in A durch B' ersetzt. (A und A' sind also strukturgleich).
Dann gilt: wenn B äquivalent mit B' ist, so ist auch A äquivalent mit A'.
([Strehl], Kap. I, Abschnitt 16)
Eine Grammatik Gt = ( Tt , Nt , Pt , St) ist Teilgrammauik von G =( T , N , P , S) , als Formalzeichen Gt ⊆ G :
Die terminalen und nicht-terminalen Symbole sowie die Produktionen müssen also ein Teil der Gesamtgrammatik sein und das Startsymbol der Teilgrammatik ist ein Nichtterminales Symbol der Gesamtgrammatik.
Beispiel: Die Grammatik der arithmetischen Ausdrücke einer Programmiersprache ist eine Teilgrammatik der Grammatik der Programmiersprache.
Beweis:
⇒ trivial.
Der Fall ⇐ ergibt sich aus der Tatsache, daß die Wörter der Teilgrammatik Teilwörter der Wörter der Grammatik sind. (Teilsprache und Teilgrammatik sind also grundverschieden.)
Sei G =( T , N , P , S) eine Grammatik und N N ein Nichtterminalsymbol.
Gesucht wird die Teilgrammatik GtN = ( Tt , Nt , Pt ,N) ⊆ G
.
L'( G,N):={w ∈ V* | N →* w} Menge der aus N ∈ N erzeugbaren Symbolfolgen
B(w) := { wi | i=1,...|w|} : Menge der Symbole im Wort w ∈ V*
W ⊆ P( V*);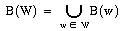 
: Erweiterung auf Wortmengen.
Die Teilgrammatik Gt N ergibt sich dann:
Tt = B(L'( G ,N)) ∩ T
Nt = B(L'( G ,N)) ∩ N
Pt = P ∩ Nt x Vt*
mit Vt := Nt ∪ Tt
St = N
(Wie man sofort sieht, ist die Teilgrammatiksbedingung erfüllt.)
Diese Konstruktion ist aber für die Theoretiker, denn die praktischen Beispiele sind einfach ersichtlich.
Im Compilerbau ist es üblich, die Schlüsselwörter, Ganzzahl und Fliesskommazahlen als terminale Zeichen zu betrachten. Der Parser empfängt diese abstrakten Eingabesymbole von einem Scanner. Damit wird erreicht, daß der Parser einfacher wird, da seine Grammatik kleiner ist.
Jedes vom Scanner erkannte Symbol stellt eine einfache Teilgrammatik dar.
Könnte man nun Teile des Scanners allgemein verfügbar machen, so sparte man sich z.B. Funktionen, die Konstanten aus einer Zeichenkette konvertieren.
Verschiedene Programmiersprachen haben die selbe Syntax für diverse Konstanten. Damit könnten Compiler für diese Programmiersprachen in einem Rechensystem Teile von ihren Scannern gemeinsam haben.
Dieses Vorgehen kann verallgemeinert werden. Beispielsweise unterschieden sich arithmetische Ausdrücke nur unwesentlich in diversen Programmiersprachen. Die arithmetischen Ausdrücke werden z.B in einem Tischrechnerprogramm (Tabellenkalkulation, Datenbanksystem,...) auch eingesetzt.
Da Teilgrammatiken wie oben angedeutet, mehrfach verwendet werden können, ist es sinnvoll sie als Objekte in einem objektorientierten Compiler zu definieren.
Ein Compiler ruft dann bei der Analyse zur Identifikation eines Unterkonstruktes eine Parserroutine einer Teilgrammatik auf.
Bei der Compilerkonstruktionsmethode des rekursiven Abstiegs von N. Wirth entstehen diese Teilgrammatikparser automatisch.
Bei attributierten Grammatiken werden die Terminal- und Nichtterminalsymbole mit Attributen versehen. Somit ist also naheliegend, diese als Klassen im objektorientierten Sinn aufzufassen. Diese aus den Symbolen induzierten Klassen sind dann auch Bestandteil der internen Strukturen das Compilers.
Die internen Strukturen, die ein Compiler zur Analyse und Optimierung verwendet, sind Kandidaten für Klassen im Sinne der objektorientierten Programmierung. Wenn Sprachen gemeinsame Teilgrammatiken haben, dann können sie auch die gleichen internen Strukturen verwenden.
Auch wenn verschiedene Sprachen verschiedene Teilgrammatiken für ein Konzept wie z.B `arithmetischer Ausdruck' haben, so könnten in Compilern ähnliche interne Strukturen haben.
Viele Optimierungsroutinen, die auf diesen Strukturen arbeiten, können dann geteilt werden.
1. Der Begriff "Menge" sei schon als konstruiert vorausgesetzt. Alternativ könnte man auch eine naive Ansammlung von Zeichen annehmen. Ebenso seien schon die Menge aller Wörter A * aus dem Alphabet A, die Relationen, die transitive Hülle einer Relation und Funktionen schon konstruiert.
2. Der Begriff `Term' müßte eigentlich eingeführt werden (z.B wie in Lor64 ), dies kann mit Hilfe einer Grammatik geschehen; der Leser wird aber sicher mathematisch vorgebildet sein, so daß hier darauf verzichtet werden kann.
